독일에서의 양자 컴퓨팅 연구 성과가 입자 물리학 분야에 혁신을 가져오며 금융, 경제, 암호화폐 분야에 중요한 영향을 미칠 수 있다. 암호화폐 산업은 이제 최고과학책임자와 입자 물리학자를 포트폴리오에 추가할 시기가 되었을지 모른다.
4일(현지시간) 코인텔레그래프에 따르면 독일의 양자 컴퓨팅 연구 성과가 금융, 경제 및 암호화폐 분야에 혁신을 일으킬 수 있는 가능성을 제시하고 있다. 2024년 8월 2일, 코인텔레그래프에 따르면, 독일 막스 플랑크 양자광학연구소의 연구진이 양자 시뮬레이터에서 오류를 안정적으로 제어하며 '양자 우위'를 달성할 수 있는 방법을 제시했다. 이로 인해 암호화폐 업계는 최고과학책임자와 입자 물리학자를 영입할 필요성이 커지고 있다.
과거 기술 산업은 자체적인 공학적 혁신과 성과에 기반하여 성장해왔다. 블록체인과 암호화폐의 발명은 개인용 컴퓨터와 인터넷의 출현과 비슷한 기술적 혁신으로 평가받고 있다. 그러나 지난 20년 동안, 기술 산업은 '하드 사이언스'에 중점을 두고 발전해왔다. 아마존, IBM, 구글, 마이크로소프트, 메타 같은 주요 기업들은 양자 컴퓨팅 연구소를 운영하며, 물리학과 양자 컴퓨팅 분야에서 중요한 연구 성과를 내고 있다.
특히 구글의 연구소에서는 2021년 양자 프로세서에서 시간 결정(Time Crystals)을 실현했으며, 마이크로소프트와 IBM은 양자 우위를 확장하기 위한 연구에 기여하고 있다. 양자 우위는 양자 컴퓨터가 고전적인 이진 컴퓨터로는 불가능하거나 유용하게 수행할 수 없는 문제를 해결할 수 있는 능력을 의미한다.
양자 컴퓨터가 다체 문제를 해결할 수 있는 능력을 갖춘다면 입자 물리학 분야에서 중요한 발전을 이룰 수 있다. 다체 문제는 수많은 입자의 움직임을 예측하는 문제로, 이는 물리학에서 가장 어려운 문제 중 하나로 여겨진다. 이러한 양자 컴퓨팅의 발전은 암호화폐 산업에도 큰 영향을 미칠 수 있다.
이코노피직스는 경제 문제를 물리학적 방법으로 해결하려는 시도로, 1990년대 초 개인용 컴퓨터가 대중화되면서 등장한 개념이다. 양자 컴퓨팅이 성숙해지면서 '크립토피직스'라는 새로운 분야가 부상할 가능성도 있다.
양자 컴퓨터가 다체 문제 해결에서 이진 컴퓨터보다 우위를 점할 수 있다면, 이는 시장 움직임을 예측하는 데 있어 현재의 슈퍼컴퓨터보다 훨씬 뛰어난 성능을 발휘할 수 있다. 비트코인(BTC) 거래는 특정 수량이 정해져 있어 양자 컴퓨터가 다체 모델 문제로 처리하기에 상대적으로 더 간단할 수 있다. 이는 양자 컴퓨팅의 발전이 암호화폐 시장 분석과 예측에 기여할 수 있는 가능성을 시사한다.
뉴스 속보를 실시간으로...토큰포스트 텔레그램 가기



















 5
5







![[암호화폐 개척자들] 여명의 시기 5화 ㅡ 어준선, 선구자의 세금을 내며 시장을 개척하다](https://f1.tokenpost.kr/2026/03/6hc0zx6flq.jpg)


![[토큰분석]](https://f1.tokenpost.kr/2026/03/1bgeh6d0t0.jpg)











![[Episode 12] IXO™2024 참여하고, 2억원 상당 에어드랍 받자!](https://f1.tokenpost.kr/2024/03/bk2tc5rpf6.png)
![[Episode 11] 코인이지(CoinEasy) 에어드랍](https://f1.tokenpost.kr/2024/02/g0nu4cmps6.png)
![[Episode 8] Alaya 커뮤니티 입장하고, $AGT 받자!](https://f1.tokenpost.kr/2023/10/0evqvn0brd.png)
![[Episode 6] 아트테크 하고, 에어드랍 받자!](https://f1.tokenpost.kr/2023/08/3b7hm5n6wf.jpg)
![[토큰포스트] 기사 퀴즈 549회차](https://f1.tokenpost.kr/2026/03/6j5ydfkdjn.jpg)
![[토큰포스트] 기사 퀴즈 547회차](https://f1.tokenpost.kr/2026/03/4i8acp5kqv.png)
![[토큰포스트] 기사 퀴즈 546회차](https://f1.tokenpost.kr/2026/03/p1jfeb06y7.jpg)
![[토큰포스트] 기사 퀴즈 545회차](https://f1.tokenpost.kr/2026/03/yzt2egy26e.jpg)






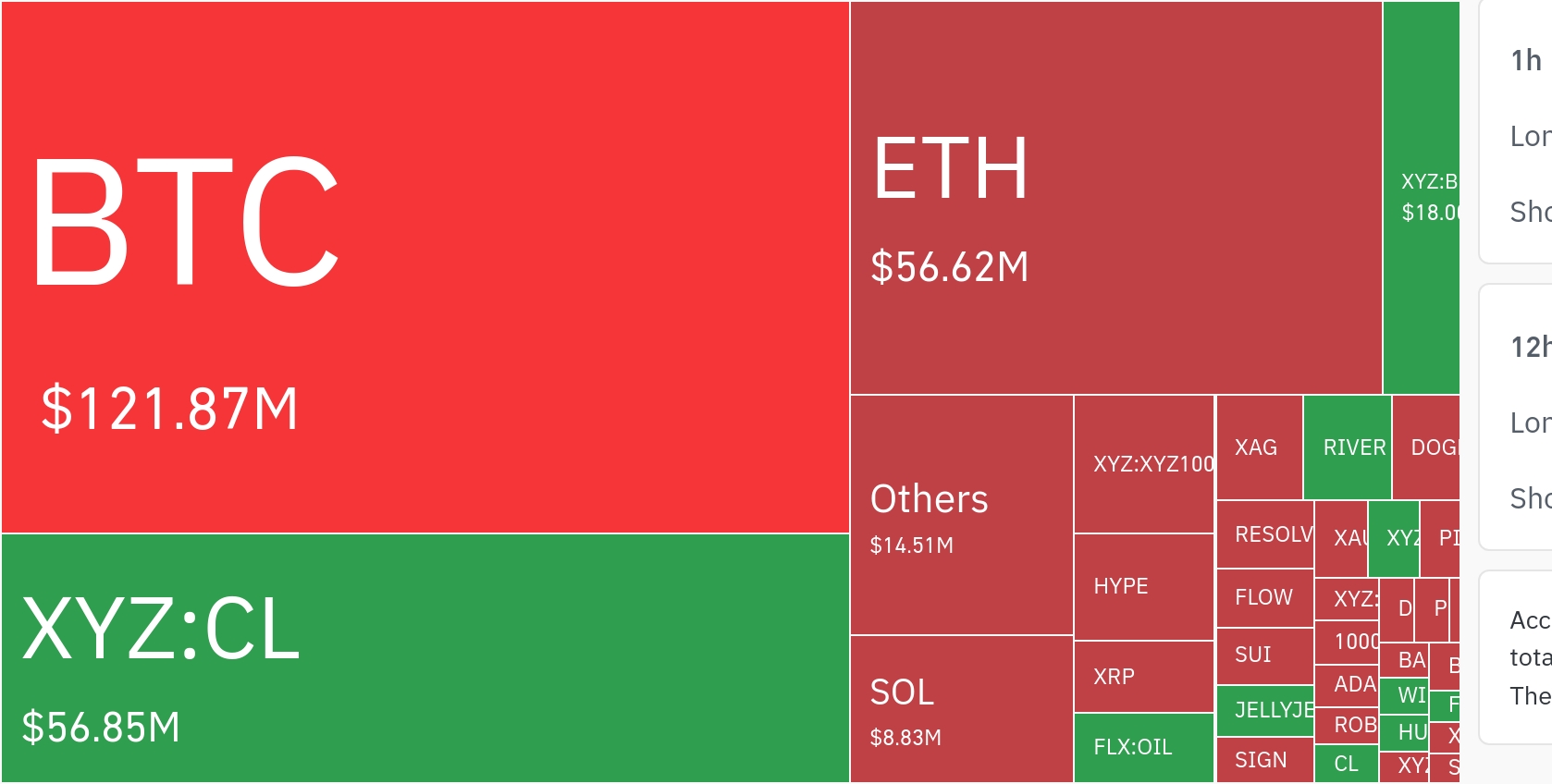

![[크립토 인앤아웃] BTC 1억2900만 달러 유입…USDC→USDT로 1억7200만 달러 이동](https://f1.tokenpost.kr/2026/03/9a9xutes55.jpg)


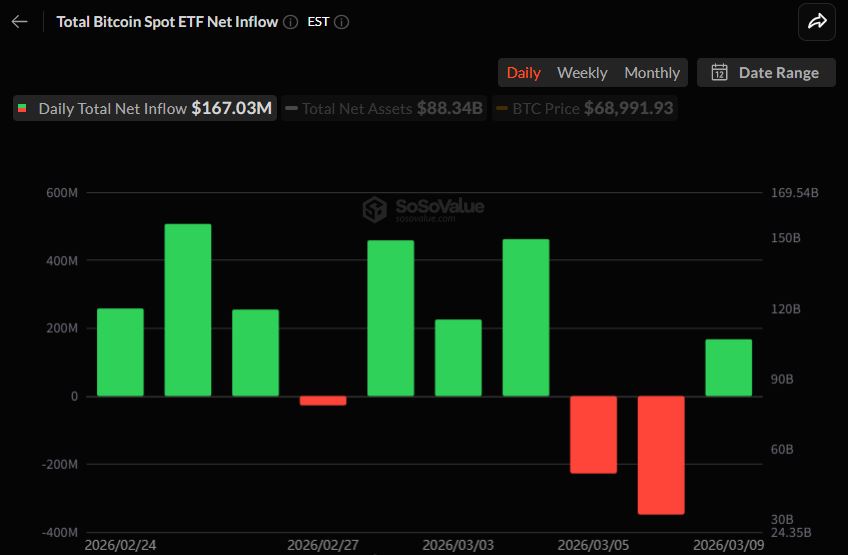
![[월가 유동성 레이더] 코인베이스 BTC 거래량 142% 급증…프리미엄 플러스 전환·순입출금 혼조](https://f1.tokenpost.kr/2025/09/gc2rcv5ndg.png)















